1.概述

强化学习是状态（state）或情形（situation）与动作（action）之间的映射，目的是最大化一些数值形式的奖赏，通过不断的学习找到规律。

2.状态和动作空间

学习器需要经历的所有可能的状态集合叫作状态空间（state space），有一个相对应的动作空间（action space）包含所有可能的动作。

3.奖赏函数

奖赏函数类似遗传算法中的适应度函数。对于情节性的（episodic）问题，学习过程将被分为许多情节，并且有一个明确的终点，比如机器人到达迷宫中心。而对于非情节性的例子（连续任务（continual task）），并且在任务停止前没有间断，比如婴儿学走路，当它不会跌倒时才算是真的学习成功，而不是10分钟内不会跌倒。

激励学习的是总共的奖赏，即从开始一直到任务结束的期望奖赏（当学习器到达最终状态（terminal state）或接受状态（accepting state））。然而，连续任务没有终结状态，所以要预测奖赏一直到无限的情况下其实是不可能的。

4.折扣

折扣（discounting）意味着我们要考虑到对于发生在未来的事有多确定：根据学习中出错的概率对未来奖赏的预测打折扣，我们可以加入额外的参数0 ≤ γ ≤ 1，通过乘以$γ^t$来对未来奖赏的预测打折，t是奖赏中未来的时间步数，γ小于1，所以γ的n次方就更小，所以可以忽略未来很远的预测。

$$R_t = r_{t+1} + \gamma r_{t+2} + {\gamma}^2r_{t+3} + ... + {\gamma}^{k-1}r_{t+k} + ... = {\sum_{k=0}^{\infty}γ^{k}r_{t+k+1}}$$ (4.1)

$\gamma$越接近0，也就对未来价值看得越近，当它等于1，就没有折扣。

5.动作选择

强化学习中，算法会查看中当前状态下可以进行的每个动作并计算每个动作的值，也就是在当前状态选择这个动作的平均奖赏，可以通过计算以前记录的每次奖赏平均值来实现，这就是$Q_{s,t}(a)$，其中s是状态，a是动作，t是以前这个动作在这个状态下被选择的次数。

三种选择a的方法：

1. 贪婪法：选择$Q_{s,t}(a)$最高的动作，利用当前知识

2. $\epsilon$-greedy：与贪婪算法相似，但有小概率会随机选择其他动作

3. soft-max：

$$P(Q_{s,t}(a))=\frac{exp(\frac{Q_{s,t}(a)}{\tau})}{\sum_{b}exp(\frac{Q_{s,t}(a)}{\tau})}$$ (5.1)

利用soft-max函数来做出选择。引入新参数$\tau$表示温度，与模拟退火有关系，当它很大时所有动作都有相似的概率；当它很小时，选项的概率就更重要。在soft-max中，大多时间会像贪婪一样，但有些情况会按照与它们估计的奖赏比率来选择，并在选择之后更新。

6.策略

动作选择旨在利用探索和开发的方法来最大化未来的期望奖赏，而另一方面，其实可以用明确的决策来时每个阶段都做最好的选择，考虑在每个状态选择哪个动作来使得结果更加优化，这就是策略（policy）。

7.马尔可夫决策过程

7.1马尔可夫性

由下棋游戏举例，当前所有棋子的位置（状态）足以预测下一步是否是好的——与每个棋子如何来到当前位置无关，那么，当前的状态就提供了足够的信息。一个状态如果具有这种性质，也就是当前的状态对于计算奖赏提供了足够的信息而不需要以前的状态信息，就称为m马尔可夫状态（Markov state）。它的重要性可由下面两个等式给出：

$$Pr(r_t = r', s_{t+1} = s'|s_t,a_t,r_{t-1},s_{t-1},a_{t-1},...,r_1,s_1,a_1,r_0,s_0,a_0)$$ (1.1) $$Pr(r_t = r', s_{t+1} = s'|s_t,a_t)$$ (1.2)

等式（1.1）是马尔可夫性不成立的条件，等式（1.2）是马尔可夫性成立的条件，可用于计算下一步的奖赏r’和状态t’。

一个满足等式（1.2）的问题称为马尔可夫决策过程（Markov Decision Process, MDP）。

7.2马尔可夫决策过程中的概率

下图是一个简单的马尔可夫决策过程例子，根据今天的心情决定明天的心情。

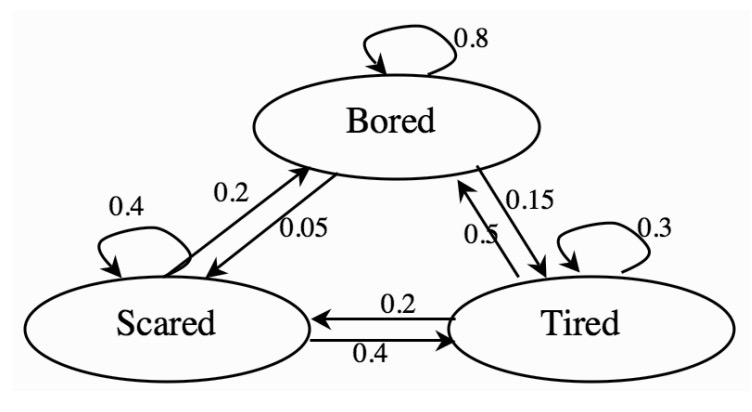
马尔可夫决策过程形式是上一个有力的解决额外不确定性的方法，例如它可以被扩展，处理真正的未知状态，只能有一个对状态的观察，概率上与状态相关，也有可能是动作，这被定义为部分观察马尔可夫决策过程（POMDP）。

8.值

两种计算值的方法：状态值函数（the state-value function）V(s)，动作值函数（action-value function）Q(s,a)。

状态值函数可以考虑当前的状态，并对所有可以采取的动作进行平均，让策略自己解决问题；动作值函数分别考虑当前的状态和每个可能的动作。

(8.1)

(8.2)

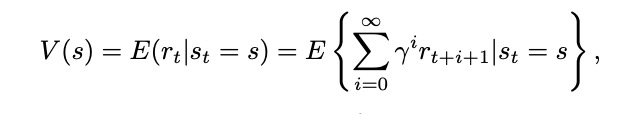
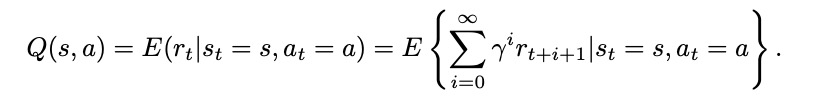
(8.2)处理更多信息，在长期运行时会更精确，但将花费很多时间学习，也就是更依赖维度。

现在我们还需要解决预测值函数和最佳策略的问题。最佳策略就是值函数值所有可能的状态中都是最大的，可以用*号标记。状态s的价值体现为：在该状态下遵循某一策略而采取所有可能行为的价值按行为发生概率的乘积求和。一个行为价值函数也可以表示为状态价值函数的形式：

(8.3)

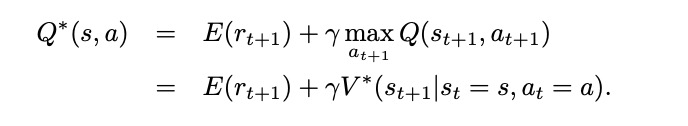
它表明，一个状态下采取某一个行为的价值分为两部分，一是离开这个状态的价值，另一部分是所有进入新状态的价值与其转移概率的乘积之和。

更新方程：

(8.4)

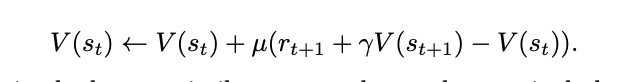
其中$\mu$是学习速率。这种使用当前和以前估计值之间的差称为*时差（TD）方法。为了判断状态是否有用，可以引入另一个参数0 ≤ λ ≤ 1，避免某个状态分量过重，也就是有效跟踪法：

(8.5)

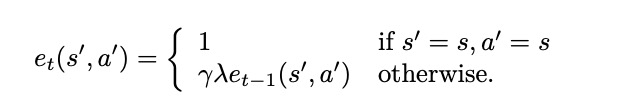
最后是Q-learning和sarsa算法：

我们可以建立奖赏矩阵R和迁移矩阵t来解决问题。

Reference:

1. Marsland S. Machine learning: an algorithmic perspective[M]. Chapman and Hall/CRC, 2014.

2. 《强化学习》第二讲 马尔科夫决策过程